MOTION GRAPHS MASTER GUIDE
Position • Velocity • Acceleration
Position–Time Graph
📐 Slope = Velocity
━ Straight line → constant velocity
⌢ Curved line → changing velocity
Velocity–Time Graph
📐 Slope = Acceleration
📊 Area = Displacement
Essential for understanding motion!
Acceleration–Time Graph
━ Flat line → constant acceleration
⎯ Line on zero → no acceleration
Key to understanding forces!
⭐ GOLDEN RULES ⭐
Slope of x–t graph gives you velocity (v)
Slope of v–t graph gives you acceleration (a)
Flat graph means no change
Curved graph means something is changing
🎯 6 MOTION CASES 🎯
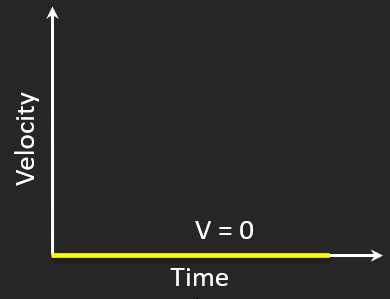
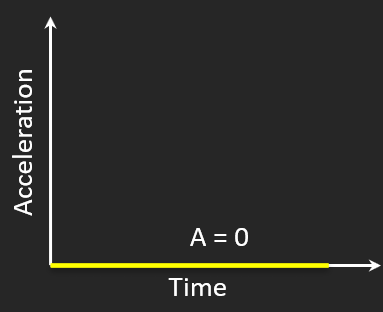
Object at Rest
💤 Position does not change
🔄 Velocity = 0
⚡ Acceleration = 0
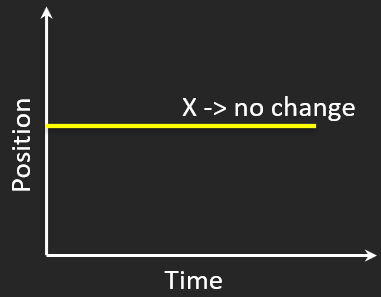
Flat x–t → zero slope → velocity is zero.
Flat v–t at zero → no acceleration.
Everything is still!
Constant Positive Velocity
➡️ Object moves forward steadily
🔄 Velocity constant
⚡ Acceleration zero
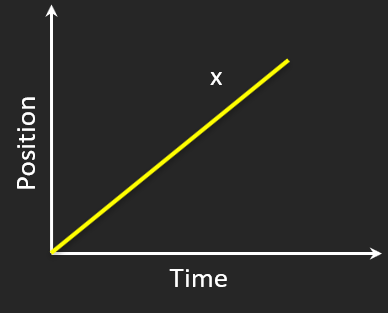
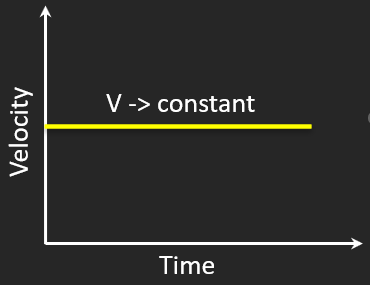

Straight slanted x–t → constant velocity.
Flat v–t → no acceleration.
Like cruise control!
Constant Negative Velocity
⬅️ Moving backward steadily
🔄 Velocity constant (negative)
⚡ Acceleration zero

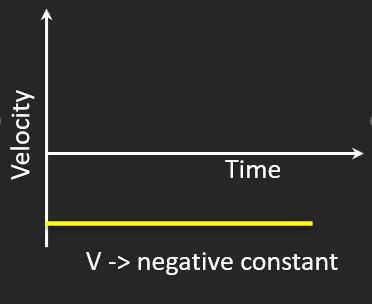

Downward slope → negative velocity. Still no acceleration.
Car reversing at constant speed!
Uniform Acceleration
🚀 Velocity increases steadily
🔄 Speed getting faster
⚡ Acceleration constant & positive
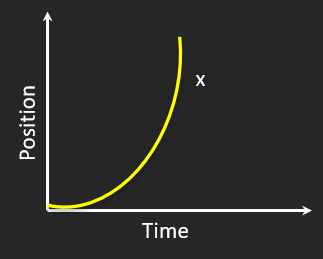
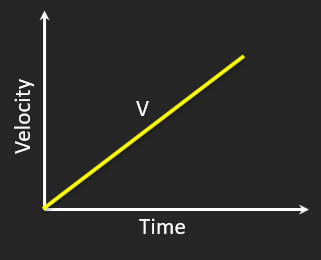

Curved x–t (getting steeper) → velocity increasing.
Straight rising v–t → constant acceleration.
Rocket launching!
Uniform Deceleration
🛑 Velocity decreases steadily
🔄 Slowing down
⚡ Acceleration negative



Curve becomes less steep → velocity decreasing.
v–t slopes downward → negative acceleration.
Car braking!
Changing Acceleration
🌀 Complex motion
🔄 Acceleration changes over time
⚡ Most realistic motion!
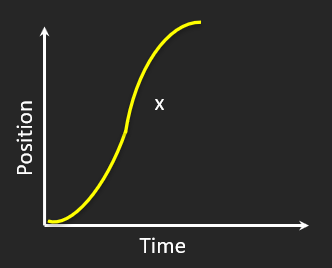


Irregular x–t → changing velocity.
Curved v–t → changing acceleration.
Real-world motion like car in traffic!
🧠 STUDENT SUPER TRICK 🧠
If you're given ONE graph, you can draw the other two easily!
Look at the slope of the graph
Ask yourself:
• Is slope constant?
• Is slope increasing?
• Is slope zero?
Apply the Golden Rules to transform one graph into another!